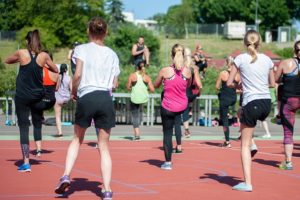Szerokie zastosowanie zamiatarek drogowych- gdzie można je spotkać?
Zamiatarki drogowe znacząco wyróżniają się na tle innych maszyn- są...
WięcejOperowanie zamiatarką drogową- czy to łatwe zadanie?
Oczyszczanie przestrzeni miejskiej to ważne zadanie, którym zajmują się wyspecjalizowane...
WięcejCo podawać dziecku, aby zdrowo się rozwijało? Czego unikać?
Zdrowe żywienie jest szalenie ważne już od pierwszych lat życia...
WięcejUprawiasz sport? To powinieneś jeść!
Osoby będące aktywne fizycznie, które trenują regularnie, powinny pozostawać na...
WięcejPowierzchnia biurowa – wynająć, kupić czy zbudować?
W dzisiejszych czasach każda dobrze prosperująca działalność gospodarcza, posiada swoją...
WięcejNa czym polega pomoc prawna w biznesie?
Pomoc prawna w biznesie może być skomplikowana do zrozumienia. Nie...
WięcejZałożenie firmy w Hiszpanii krok po kroku
Rachunkowość to złożona dziedzina, która może być trudna do zrozumienia....
WięcejPrzestrzenie biurowe w Krakowie – jak wybrać odpowiednie miejsce?
Kraków to jedno z najatrakcyjniejszych miast w Polsce, które jest...
WięcejBiuro księgowe w Hiszpanii
Chciałbyś otworzyć filię swojej firmy za granicą? Pod względem podobieństwa...
WięcejProducent wyrobów gumowych
Jako producent wyrobów gumowych, który posiada wieloletnie doświadczenie, jesteśmy w...
WięcejKarboksyterapia – działanie mechaniczne
Komórki tłuszczowe, są niezwykle bardzo uwrażliwione na iniekcje dwutlenku węgla....
WięcejBiuro dla agencji reklamowej- jakie powinno być?
Wygląd miejsca, w którym każdego dnia spędzamy wiele długich godzin...
WięcejW jaki sposób kształtują się stawki VAT w Hiszpanii?
Jeśli chodzi o wysokość stawek VAT w Hiszpanii, warto wiedzieć,...
WięcejPomoc prawna w prowadzeniu firmy- kiedy jest potrzebna?
Początkowo może się wydawać, że pomoc adwokata nigdy może nie...
WięcejJak urządzić stylowe, funkcjonalne oraz nowoczesne biuro dla swojej firmy?
Właściciele firmy, którzy nie chcą inwestować zbyt dużych pieniędzy w...
WięcejSocial media- jak wykorzystać ich potencjał?
Media społecznościowe mają w sobie ogromny potencjał, zazwyczaj jednak, aby...
WięcejKiedy wynajem biura pod działalność gospodarczą ma sens?
Biuro dla firmy można wynająć tak naprawdę zawsze, kiedy tylko...
WięcejKampania na Twitterze- czy to ma sens?
Niektórzy przedsiębiorcy sami dostrzegają ogromny potencjał mediów społecznościowych i tym...
WięcejDlaczego warto być obecnym w social mediach?
Niektórym wydaje się, że ta obecność w social mediach nie...
WięcejProwadzenie firmy- czy jest to łatwe zadanie?
Kiedy myślimy o prowadzeniu firmy zazwyczaj fakt ten kojarzy się...
WięcejKampania reklamowa- od czego zacząć?
Bez wątpienia w każdej działalności przedsiębiorstwa, ważną rolę odgrywają podejmowane...
WięcejCzy raporty są ważne?
Jeżeli zależy Wam na uzyskaniu dobrych wyników sprzedaży oraz stałym...
WięcejJak skutecznie prowadzić firmę?
Wielu właścicieli mniejszych lub większych przedsiębiorstw, często zadaje sobie pytanie...
WięcejAnaliza danych- na czym polega?
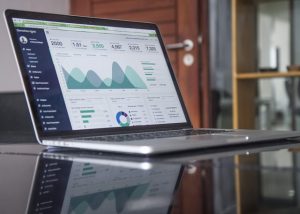
W dzisiejszych czasach na rozwój firmy składa się wiele czynników...
WięcejTablica magnetyczna suchościeralna – jaka rama do domu, a jaka do biura?
Tablice suchościeralne to niezwykle przydatny sprzęt do każdego biura. Ilość...
WięcejWłasna firma w Hiszpanii – od czego zacząć?
Założenie własnej firmy w Hiszpanii dla wielu osób jest szansą...
Więcej